Separately Excited

A separately excited DC motor is rotated at 1000rpm and the variation of armature terminal voltage as a function of field current is measured under open-circuit conditions and tabulated below:

The field winding is supplied with a constant voltage \(V_F=24V\) and the field resistance is adjustable. The armature winding resistance \(R_A=0.2\Omega\), and the armature terminal voltage \(V_T=130V\). Friction and windage losses can be neglected.

1. Calculate the field current if the motor is operated with no-load at 1000 rpm
2. The motor drives a load at 1200 rpm. Calculate the armature voltage at 1200 rpm if the field resistance \(R_F=60\Omega\)
3. Calculate the torque for the above condition
4. Maintaining the terminal voltage constant, the field current is adjusted until the motor is operating at steady state, supplying a mechanical load of 4160W at 1450 rpm. Calculate the efficiency.

Comments

This question is similar to many DC machine questions and falls into two parts. At the start of the question, you are given a reasonable amount of data about a specific operating condition. You need to then take useful information from this operating condition and apply it to the new operating conditions specified in the rest of the question.

Solution

This is a separately excited motor problem:

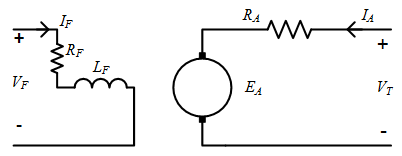
There are two important pieces of information in the beginning of the question:

• The information is being given for open circuit conditions. In this case, there is no armature current, \(I_A=0\) and therefore the terminal voltage equals the armature voltage: \(E_A |_{1000}=V_{T_{oc}} |_{1000}\)
• You are being given data on the induced armature voltage at a specific known speed. Because \(E_A\) is a function of speed, we use the notation \(E_A |_{1000}\) to explicity note that the data is valid for only one speed, 1000 rpm.

Knowing how the data in the question is useful is a significant part of the solution process for DC machine questions.

1. This asks about a condition where the motor is operating under no-load at the same speed as the data was tabulated. No-load operation with negiligble friction and windage loss means that the motor is producing no torque. Therefore there is no armature current, \(I_A=0\), and \(V_T=E_A|_{1000}=130\). From the table under open circuit conditions, \(E_A\big|_{1000}=130V\) occurs when \(I_F=0.7A\)

2. The motor is no-longer operating at 1000 rpm. Armature voltage is given by

   \[E_A=k\phi \omega_m\]

   i.e. voltage is a function of \(k\phi\) and speed. Flux is only a function of field current, and since field voltage and resistance are specified in the question, a first step is to find field current:

   \[ V_F=I_F R_F \]

   gives \(I_F=0.4A\)

   From the table in the question, when: \(n_m=1000\text{rpm}\) and \(I_F=0.4A\) then \(E_A=102V\). We need to find \(E_A\) for the case when \(n_m=1200\text{rpm}\) and \(I_F=0.4A\)

   There are two possible approaches:

   1. In both cases, the field current is constant, therefore flux will be constant. Armature voltage will be proportional to speed:
      \[ E_A |_{1200}=E_A |_{1000}\frac{1200}{1000} \]
      Giving \(E_A=122.4V\)
   2. Using the armature voltage equation and the table data, find \(k\phi\) at \(I_F=0.4A\). The data in the table gives \(E_A|_{1000} = 102V\) with \(n_m=1000 rpm\) and therefore \(\omega_m=1000\frac{2\pi}{60} = \frac{100\pi}{3}\). Therefore
      \[ \begin{aligned} k\phi |_{I_F =0.4} &=\frac{102}{\frac{100 \pi}{3}} =\frac{306}{100}\frac{1}{\pi}\\ k\phi |_{I_F =0.4} &=0.974 \end{aligned} \]
      Now, at 1200 rpm armature voltage can be found directly from the armature voltage equation:
      \[ \begin{aligned} E_A |_{1200} &=k\phi |_{I_F =0.4} \omega_m \\ \omega_m & = 1200\frac{2 \pi}{60} = 40\pi \end{aligned} \]
      Giving \(E_A=122.4V\)
3. To find the torque, there are three possible approaches.
   1. Consider the impacts of the speed changes on the circuit.
      \[ \begin{aligned} V_T&=E_A+I_A R_A\\ I_A&= \frac{V_T-E_A}{R_A} = 38.0A \end{aligned} \]
      Using power equations:
      \[ \begin{aligned} P_{conv} & =\tau \omega_m = E_A I_A \\ \tau & =\frac{122.4 \times 38.0 }{1200\frac{2\pi}{30}} \end{aligned} \]
      \(\tau=37Nm\)
   2. Using the torque equation directly: \(\tau=k\phi I_A\). This approach requires the calculation of \(k\phi\),if not already done in the armature voltage calculation, and the calcualtion of \(I_A\) as shown above.
      \[ \begin{aligned} \tau & = k\phi |_{I_F =0.4} I_A \\ \tau & = \frac{306}{100}\frac{1}{\pi} 38 \end{aligned} \]
      \(\tau=37Nm\)
   3. Rearranging the torque-speed equation:
      \[ \begin{aligned} \omega_m &=\frac{V_T}{k\phi}-\frac{R_A}{(k\phi)^2}\tau \\ \tau &=\frac{\left(k\phi\right)^2}{R_A}\left( \frac{V_T}{k\phi}-\omega_m\right) \end{aligned} \]
      \(\tau=37Nm\)

   Comment:

   Of the three approaches above, the first and second give some kind of understand that as speed changes, the internal induced voltage \(E_A\) changes, influencing \(I_A\) which in turn impacts torque. This is the logical understanding of the physical mechanisms in the machine. The last approach mathematically gives the correct answer, but gives less understanding of the entire machine response to speed and load changes.

4. In the final part of the question no information is available on the flux in the machine. The preferred approach is to consider the power in the armature circuit:

   \[ V_T I_A = E_A I_A+ I_A^2 R_A \\ \therefore I_A^2 R_A - V_T I_A +P_{conv} =0 \\ 0.2 I_A^2 - 60 I_A + 4160 = 0 \]

   Solving the quadratic for armature current results in two values, \(I_A=616A\) or \(IA=33.75A\). The correct answer will be the one that results in the lowest power loss,\(I_A=33.75A\).

   At this point, the armature losses can be found, but this is a separately excited machine and it is important to remember to account for power flow in the field circuit. It is therefore necessary to find the field circuit current \(I_F\) and again, there are mulitple approaches to this solution

   1. Find the armature voltage at 1450 rpm \(E_A|_{1450}\), scale back to \(E_A |_{1000}\) and use the table to look up \(I_F\)
   2. Calculate the torque to obtain \(k=phi\) and then calculate the corresponding value in the table
   1. \[ V_T = E_A+ I_A R_A \]
      gives\(E_A|_{1450}=123.25A\)
      \[ E_A\big|_{1000}=E_A\big|_{1450}\frac{1000}{1450} \]
      gives \(E_A\ |_{1000}=85.0V\) which, from the table, corresponds to a field current \(I_F=0.3A\)
   2. \[ \begin{aligned} P_{conv} & =\tau \omega_m \\ \tau& = \frac{4160}{\frac{1450\pi}{30}} = 27.4Nm \\ k\phi & = \frac{\tau}{I_A} = 0.812 \\ E_A|_{1000} &=k\phi \frac{1000 \pi}{30} \end{aligned} \]
      which gives \(E_A\ |_{1000}=85.0V\) which, and corresponds to a field current \(I_F=0.3A\)

   Finally, efficiency can be found from

   \[ \begin{aligned} \eta &=\frac{P_{conv}-P_{FW}}{P_{conv}+P_{RA}+P_F} \\ P_{RA}+P_F&=I_A^2 R_A +I_F^2 R_F= 235W \\ P_{FW}&=0\\ \eta &=\frac{4160}{4395} \\ \end{aligned} \]

   giving \(\eta=94.7\%\)

Series Motor Example

A series DC motor has combined armature and field resistance of \(R_A+R_S=1.2 \Omega\). When connected to a supply of \(V_T=48V\) at standstill, the motor develops a torque of 1500Nm.

1. Calculate the armature current at standstill and combined motor constant \(kc\)
2. Calculate the torque when the speed is 500 rpm
3. Calculate the output power and efficiency when operating at 500 rpm (neglect mechanical losses)

Solution

This is a series motor problem:

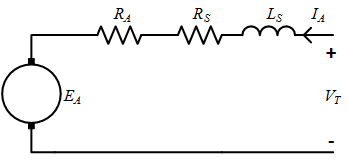
1. At standstill, the angular velocity is zero, therefore the armature voltage is zero \( E_A=kcI_A\omega =0 \). The full terminal voltage is dropped across the winding resistances and \(V_T=I_A(R_A+R_S) \) gives \(I_A=40A\). Using the torque equation for a series excited DC machine, \( \tau=kcI_A^2\), the combined motor constant can be found: \( kc=1500/1600=0.9375 Nm A^{-2} \)
2. To find the torque it is possible to either substitute directly into the series motor torque-speed equation, or to first find the armature currents:
   1. \[ \begin{aligned} \omega_m & = \frac{V_T}{\sqrt{kc}}\frac{1}{\sqrt{\tau}}-\frac{R_A+R_S}{kc} \\ \omega_m & =n_m\frac{2 \pi}{60} =\frac{50\pi}{3} \end{aligned} \]

      Re-arranging the torque speed equation and submitting for kc and speed gives \(\tau=0.854Nm\)

   2. Alternately, substitute \( E_A = kcI_A \omega_m \) into in the armature loop equation to obtain \(V_T=I_A(kc\omega_m +R_A+R_S) \) and solve for armature current. \(I_A=0.955A\) and use the torque equation \(\tau=kc I_A^2\) to obtain \(\tau=0.854Nm\)
3. To find efficiency neglecting rotational losses, in a series excited machine it is valid to use \(P_{in}=V_T I_A\):
   \[ \eta=\frac{P_{conv}}{P_{in}} = \frac{E_A I_A}{V_T I_A} = \frac{E_A}{V_T} \]
   \(\eta=97.0 \%\)