Induction Machine Equivalent Circuit Model
We have seen that induction machines (as you might guess from the name) operate on the principle of induced currents. There are still two magnetic fields, one from each of the rotor and stator, but the rotor field is induced by the stator field. Effectively, we can think of the induction machine as a rotating transformer. The stator is like the primary of a transformer and creates the initial field, inducing voltages and currents in the secondary rotor winding. The fundamental differences from a stationary transformer are:
- The secondary rotates
- There is an airgap, therefore more mmf is needed for a given flux density
- The secondary voltage and frequency depend on speed
As an aside, a wound rotor induction machine can actually be used as a variable frequency transformer. For instance, a 60Hz system connected to the primary of an induction machine can transfer power to a 50hz system connected to the rotor if the machine is mechanically driven at a slip of 5/6.
The per-phase equivalent circuit model for an induction machine in steady state operation supplied by a balances three-phase supply is based on the transformer model shown in Fig. 1.
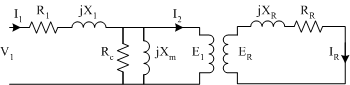
In Fig. 1.,
- V1 = Phase RMS Voltage
- I1 = Stator Phase Current
- R1 = Stator Winding Resistance
- X1 = Stator Winding Leakage Reactance
- Xm = Magnetizing Reactance
- Rc = Core Loss Resistance
- E1 = Air Gap Voltage
- I2 = Rotor Current Referred to Stator
- ER = Rotor Induced Voltage (Actual)
- IR = Rotor Current Voltage (Actual)
- XR = Rotor Leakage Reactance (Actual)
- RR = Rotor Resistance (Actual)
Rotor Circuit
We know from the operating principles that induced voltage \(E_R\) and rotor leakage reactance \(X_R\) both depend on slip. To simplify the model we can define them both in terms of their values when the speed is zero, slip \(s=1\)
where
- \(E_{R0}\) is the induced voltage at standstill
- \(X_{R0}\) is the rotor leakage reactance at standstill
With the above definitions we can write the equation for actual rotor current as
and the transformer model may be re-drawn as shown in Fig. 2
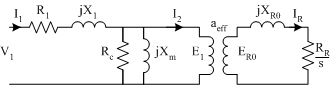
In Fig. 2, the effective turns ratio \(a_{eff}\) is constant and equal to the effective turns ratio at standstill. In a wound rotor machine, \(a_{eff}\), \(R_R\) and \(X_{R0}\) can be measured. In a cage machine these parameters cannot be directly determined, there is no method to directly measure voltages or currents on the rotor. To overcome this difficulty, the rotor (secondary) circuit can be referred to the stator (primary) side.
Full Equivalent Circuit Model
Referring the rotor circuit to the primary the induction motor per-phase eqiuvalent circuit, shown in Fig. 3. is obtained.
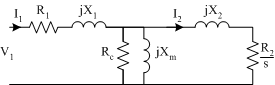
In the above circuit
- \(R_2=a_{eff}^{2}R_R\), is the rotor resistance referred to the stator
- \(X_2=a_{eff}^{2}X_{R0}\), is the rotor leakage reactance referred to the stator
The symbols used in induction machine models vary depending on the text and the context in which the circuit is being used. \(R_I\), \(R_o\), \(R_{fe}\), \(R_m\) can all be found as references to the iron loss resistance. In some texts (especially from Europe), \(R_2\). \(X_2\) refer to actual rotor values with \(R'_2\), \(X'_2\) used for referred values. In drives texts, it is common to find \(R_s\), \(R_r\) for stator resistance and rotor resistance referred to the stator with \(X_{ls}\), \(X_{lr}\) for stator and rotor leakage reactance.
Power Flow
The input power to a three-phase induction machine is given by
Output power can be found by subtracting the losses from the input power
Losses
- Stator Copper Loss. The stator resistive losses
\[ P_{SCL}=3I_1^2R_1 \]
- Rotor Joule Loss. The rotor resistive losses. This is often called rotor copper loss, but since the
rotor conductors are aluminum, rotor joule loss is the more correct terminology.
\[ P_{RCL}=3I_2^2R_2 \]
- Core Loss, or Iron Loss. The losses due to eddy current and hysteresis losses in the laminations. This can be calculated using the resistor \(R_c\). At times, core losses are grouped with friction and windage and stray loss as rotational losses.
Rotor Power
The power transferred to the rotor is called the "Airgap Power". Consider the equivalent circuit below (the core loss resistance has been removed and core losses grouped into rotational loss).
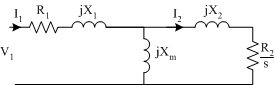
From the above circuit, the total power transfer to the rotor is given by
To find the power converted to the mechanical system the rotor joule loss must be subtracted from the total rotor power
From the above equations, it can be seen that power converted to the mechanical system is a function of the airgap power and slip:
Final output power may be obtained by subtracting the rotational loss from \(P_{conv}\).
Summary
The induction machine per-phase equivalent circuit developed on this page is valid for steady state analysis of an induction machine with a cage rotor, when connected to a balanced supply. It is used extensively in induction motor analysis. The equations for air gap power and the power convertered to mechanial energy are used extensively in induction motor analysis.