Power and Torque

Using the simplified generator power flow diagram it can be seen that the difference between mechanical input power and electrical ouput power is the combined rotational loss plus \(I^2R\) losses. If the field currend is provided by a pilot exciter and synchronous exciter, the power for the rotor \(I^2R\) losses is supplied from the mechanical system and may be grouped with rotational losses.

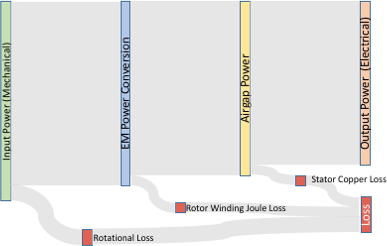
Simplified Generator Power Flow
Fig. 1. Simplified Generator Power Flow

Power converted, \(P_{conv}\)is the product of electromagnetic torque and speed

\[ P_{conv}=\tau \omega_s \]

and will equal the power delivered to the armature circuit. Power and torque equations for balanced synchronous generators can then be obtained from analysis of the per-phase equivalent circuit and phasor diagram.

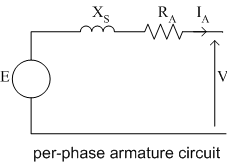
armature equivalent circuit model
Fig. 2. armature per-phase equivalent circuit model

From the above circuit, the electrical output power output from one phase may be written as

\[ P_{1\phi}=VI_A \cos \theta \]

For three phases Power and Reactive Power are given by

\[ \begin{aligned} P_{out} & =3VI_A \cos \theta \\ Q = & =3VI_A \sin \theta \\ \end{aligned} \]

The electrical input power can be found from either the real part of the product of induced voltage phasor and armature current phasor or the output power plus armature Ohmic losses:

\[ P_{conv}=P_{out}+3I_A^2R_A \]

Approximations with negligible resistance

In large machines, the resistive losses in the machine are small as a percentage of the total power flow. (Note this does not mean they are small, 1.0 percent resistive loss in a 100MW machine is still 1MW losses and cooling must be designed accordingly). For approximate analysis purposes, resistive losses can be neglected and input power will equal output power. The phasor diagram is also simplified accordingly:

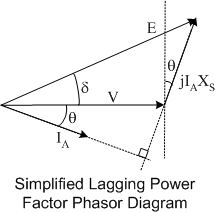
simplified phasor diagram
Fig. 3. Simplified phasor diagram drawn at lagging power factor

From the above diagram it can be seen that

\[ \begin{aligned} E \sin \delta & = I_A X_S \cos \theta \\ E \cos \delta - V & = I_A X_S \sin \theta \end{aligned} \]

and therefore

\[ \begin{aligned} P & =\frac{3VE}{X_S}\sin \delta \\ Q &=\frac{3VE}{X_S}\cos \delta -\frac{3V^2}{X_S} \end{aligned} \]

Using the equation for power conversion, the torque may be written as

\[ \tau=\frac{3VE}{X_S \omega_s} \sin \delta \]

In the above equations, \(\delta\) is defined as the load angle.

The simplfied torque and power equations show that the electromagnetic torque is propotional to the sine of the angle bewtwen the open circuit voltage \(\vec{E}\) and the terminal voltage \(V\). This angle is called the load angle. The principle that torque is proportional to the sine of the load angle is very important to the operation of round rotor generators (i.e. turbo generators).